وقتی بچه بودیم، از کنار هم گذاشتن تکه های کوچک، شکل های مختلف می ساختیم. اگر زرنگ بودیم، وقتی به مستطیل نیاز  داشتیم و لگو مستطیل را نداشتیم. مثل شکل زیر با دو مثلث قائم الزاویه یک مربع و با دو تا مربع یک مستطیل می ساختیم. می توانستیم لوزی یا ذوزنقه هم با مثلث بسازیم. خلاصه مثلث، پایه ی تمام شکل های ما بود.
داشتیم و لگو مستطیل را نداشتیم. مثل شکل زیر با دو مثلث قائم الزاویه یک مربع و با دو تا مربع یک مستطیل می ساختیم. می توانستیم لوزی یا ذوزنقه هم با مثلث بسازیم. خلاصه مثلث، پایه ی تمام شکل های ما بود.
اگر یک شکل را با مثلث نمی توانستیم، بسازیم نگاه می کردیم، که پایه لازم برای ساختن آن شکل چیست. خلاصه شکل های مورد نظر خود را از کنار هم گذاشتن قطعات پایه می ساختیم.
تا اینکه رفتیم راهنمایی و دبیرستان، توی دبیرستان بردار یاد گرفتیم. دوباره به ما گفتند، همه بردارهای روی صفحه را می توان با کمک دو بردار پایه ساخت. ( بردار های فضائی را با سه بردار پایه و بردار های n بعدی را با n بردار پایه می توان ساخت.) مثل شکل زیر که ساخت بردارهای دو بعدی را به کمک بردارهای پایه نشان می دهد. قبول دارید که با هزاران بردار قرمز به تنهایی نمی توان بردار آبی را ساخت. چون وقتی با چند بردار قرمز به جلو رفتیم، باید راهمان را کج کنیم و عمود بر مسیر قرمز برویم. یعنی از یک بردار عمود بر بردار قرمز استفاده کنیم. بردارهای پایه ما باید عمود برهم ( متعامد ) باشند.
اما نمی دانم چرا بعضی از ما فکر نمی کردیم لگو بازی می کنیم، یادگرفتنش برای ما سخت شده بود. در حالی که این بار برای مان 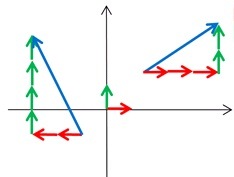 فایده داشت. ما برای جمع، تفریق و یا ضرب دو بردار کج و بی قواره، کافی بود با دو بردار کوچولوی قشنگ کار کنیم و فقط چند عدد را با هم جمع یا در هم ضرب کنیم، که آن را هم کلاس سوم دبستان یاد گرفته بودیم.
فایده داشت. ما برای جمع، تفریق و یا ضرب دو بردار کج و بی قواره، کافی بود با دو بردار کوچولوی قشنگ کار کنیم و فقط چند عدد را با هم جمع یا در هم ضرب کنیم، که آن را هم کلاس سوم دبستان یاد گرفته بودیم.
بله حق با شماست، ما فایده جمع ، تفرق و ضرب دو بردار را نمی دانستیم. یا هم فکر نکرده و یا دوست نداشتیم بدانیم چه کاربردهایی دارد. باور کنید از صنعت اتومبیل، هواپیما، کشتی، ساختمان، نجوم و ماهواره گرفته تا بازکردن یک پیچ و زدن یک مشت توی یک دعوا کاربرد دارد.
رفتیم دانشگاه و یک روز سر کلاس ریاضی مهندسی استاد درس بی مقدمه فرمول های زیر را روی تخته نوشت. گاهی هم نیم نگاهی به کاغذهای دستش می کرد، انگار او هم در طول عمرش جز نوشتن روی تخته، این فرمول ها به کارش نیامده بود. خیالمان راحت شد که دوای یادگرفتن این فرمول ها یا تقلب است و یا با هر جون کندنی حفظ برای دو ساعت جلسه امتحان.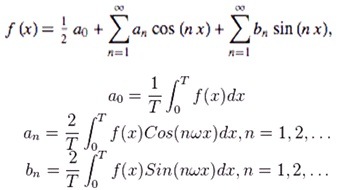
گفت اگر تابع ( f(x یک تابع متناوب و انتگرال آن در دوره تناوب محدود باشد و تعداد مینیمم و ماکزیممها و ناپیوستگی های آن محدود باشد، می توان آن را با یک سری توابع پایه (سینوسی و کسینوسی) نوشت ( ای کاش به جای کلمه "نوشت"، کلمه "ساخت" را به کار ببریم.)، به گونه ای که ضرایب a و b از فرمول های زیر بدست می آید. اگر تابع فرد باشد ضرایب a صفر می شوند، اگر تابع زوج باشد..، اگر تابع این باشد...، اگر تابع آن باشد...، ...
بعد هم چند شکل مثلثی, دندانه اره ای، مربعی و... کشید و ضرایب a و b را بدست آورد و چند تمرین هم به ما معرفی کرد تا ما هم از فیض محاسبه a و b ها بی نصیب نباشیم. خلاصه یک ساعت و نیم او می گفت و می نوشت و ما روی صندلی ها نشسته بودیم و هر از گاهی از خستگی، خود را جابجا می کردیم. هیچ کس نمی دانست این ها به چه دردی می خورد. به فکرش هم نمی رسید که می توان با آن ها صاحب آب و نان شد و راحت زندگی کرد. بچه ها سرکلاس که یا نمی فهمیدند ( که احتمالاً بعید است، چون مطلب ساده ای است و قوانین ماکسول و محاسبه انتگرال روی سطوح کروی نیست ) و یا با قضاوت اینکه این ها نان و آب نمی شود، هر کدام توی رویای خودشان بودند.
اما یکی از بچه ها شنیده بود، که تبدیل فوریه اگر پر کاربردترین موضوع ریاضی نباشد، حداقل جزو پرکاربردترین مباحث ریاضی در مهندسی، فیزیک، پزشکی، هواشناسی، مخابرات، پردازش سیگنال و... است.
واقعاً فوریه چه می گوید: ( اگر کمی دقت کنید همان قضیه لگو بچگی و بردار دبیرستان است.)
وقتی ما صحبت از سیگنال می کنیم، همان f(x) ریاضیدان ها است. سیگنال ها در واقعیت مانند مثال های درس مدار و الکترونیک یک موج سینوسی تر و تمیز نیستند، حالا بهتر است بگویم یک تک فرکانس نیستند. بلکه شامل چندین سینوسی با دامنه و فازهای مختلف هستند، که با هم ترکیب شده اند و ظاهرشان شبیه یک موج سینوسی نیست. شکل زیر دو نما از یک سیگنال را نشان می دهد. نمای راست سیگنال را در حوزه زمان نشان می دهد. همان طور که می بینید، با نگاه کردن آن چیزی دستگیرمان نمی شود. حال بیایید، این ببینیم این سیگنال از چه ساخته شده است. بله خواهیم دید که از ترکیب ( جمع ) چند سیگنا سینوسی ساخته شده است. فوریه نشان می دهد که همه توابع متناوب ( با چند شرط ) را می توان از ترکیب توابع پایه سینوسی ساخت. فرمول های بالا طرز بدست آوردن این توابع پایه هستند. البته برای اینکه سیگنال های غیر متناوب و گسسته را نیز بتوان بر اساس توابع پایه بیان کرد، تبدیل فوریه و تبدیل فوریه گسسته به کمک ما می آید.
حال بیایید سیگنال بالا را از نمای چپ، که نشان دهنده توابع پایه سینوسی موجود در سیگنال است ببینیم. ، واقعاً جالب است. این سیگنال شامل سه تابع سینوسی پایه است. نگاه چپ اطلاعات زیادی به ما می دهد. نگاه چپ، نگاه در حوزه فرکانس است، و محور افقی همانطور که می بینید، فرکانس است و زمان نیست. باور می کنید که با ترکیب این سه فرکانس می توان سیگنال اولیه را ساخت. پس از تبدیل فوریه برای پردازش و ساخت سیگنال ها می توان استفاده کرد.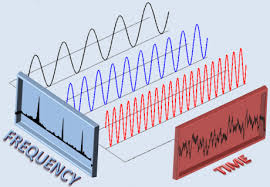
من نگاه به حوزه فرکانس و حوزه زمان، را تشبیه به آدم با سواد (بینا) و بی سواد (نابینا) می کنم. یک آدم بی سواد وقتی این نوشته ها را نگاه می کند، جز چند خط سیاه نمی داند، ولی برای یک باسواد هر کلمه معنی دارد.
سری فوریه و تبدیل فوریه ( پیوسته و گسسته ) به ما نگاه جدید و امکان پردازش قوی می دهد. نمایش سری فوریه زیر نیز زیباست.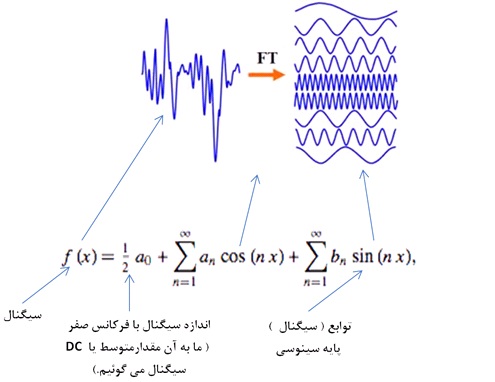
حالا فرمول بالا برایتان زیباتر نشد؟!
بیایید صدای خودمان را روی اسیلوسکوپ مشاهده کنیم، چیز زیادی دستگیرمان نمی شود، شاید فقط بتوان از حداقل و حداکثر دامنه آن حرف زد. شکل موجهای زیر فقط دو آوای 'ee' و 'oh' هستند.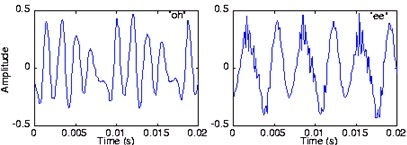 ما در رشته مهندسی به کمک اسیلوسکوپ این سیگنال ها را می بینیم. همانطور که در شکل بالا می بینید، در اسیلوسکوپ، محور افقی زمان و محور عمودی اندازه است. بیایید از زاویه دیگری به این سیگنال ها نگاه کنیم و ببینیم این سیگنال از ترکیب چه فرکانس هایی ( شکل موج های سینوسی ) تشکیل شده است.
ما در رشته مهندسی به کمک اسیلوسکوپ این سیگنال ها را می بینیم. همانطور که در شکل بالا می بینید، در اسیلوسکوپ، محور افقی زمان و محور عمودی اندازه است. بیایید از زاویه دیگری به این سیگنال ها نگاه کنیم و ببینیم این سیگنال از ترکیب چه فرکانس هایی ( شکل موج های سینوسی ) تشکیل شده است.
حال بیایید، طیف فرکانسی شکل موج های بالا را ببینیم.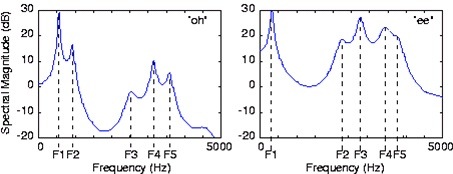
بله آوای 'oh' شامل فرکانس های F1 تا F5 با دامنه های مشخص شده است و با فرکانس های آوای 'ee' فرق می کند. ما با مقایسه این فرکانس ها می توانیم، این آوا ها را از یکدیگر تمیز دهیم. تازه اگر بخواهیم می توانیم با ترکیب این فرکانس ها، آواهای فوق را ایجاد و از بلندگوی کامپیوتر ( سیستم میکروکنترلر AVR ) پخش کنیم.
امیدوارم با این مقدمه کمی ارزش و کاربرد سری فوریه را نشان داده باشم.
کاربردهای تبدیل فوریه : ( از نظر من همه چیز )
- پردازش سیگنال ( صوت، تصویر، قلب، مغز و...)
- طراحی فیلترها و کنترل کننده ها
- تبدیل ها، کدینک و انکدینگ
- پردازش و آنالیز داده
- طراحی فرستنده، گیرنده و آنتن ها
- شناسایی سیستم ها
- همبستگی توابع
- پزشکی
-
این هم یک شکل از تبدیل فوریه چند بعدی سیگنال مغز :